Our time machine that we developed in part one and part two still needs some explanation, so let’s dive in.
First Things First: The MAXX Wasn’t Needed
Looking back, I noticed that I was overcomplicating things needlessly. The final formula I had involved the following FILTER() term, in which I used a MAXX:
FILTER(ALL(Periods),
Periods[NextYear Period]<=
MAXX(VALUES(Sales[Period Num]), Sales[Period Num])
)
Turns out that MAX() works just fine, so let’s replace that clause and simplify things a bit. Here’s the new formula:
CALCULATE([Total Sales],
ALL(Periods),
FILTER(ALL(Periods),
Periods[Year]=MAX(Periods[Year])-1
),
FILTER(ALL(Periods),
Periods[NextYear Period]<=MAX(Sales[Period Num])
),
VALUES(Periods[MerchPeriod])
)
OK, with that, we can move on to explanation: How does this formula work??
I used to call this technique “expand then filter”
Well actually I still do, in my own head. It’s just that the GFITW is a catchier title.
OK, so the “expand” part is just that first ALL():
CALCULATE([Total Sales],
ALL(Periods),
The first step in the formula, then, is basically just telling the calc engine to throw away all filters on the Periods table. In other words, “forget all concept of time, pretend the pivot is not filtered at all with respect to time.”
We do this so that we have a clean slate. Then, in the subsequent FILTER clauses, we build up a new filter context for time.
One more time for clarity: the way this formula works is to first throw out all time filters, and then in subsequent steps, we build up new filters to match the time period that we want, which in this case is last year.
Once you understand that, this overall formula starts to get pretty simple. Each piece of the formula is quite straightforward in its own right. ALL() is pretty straightforward for sure, and so are the subsequent FILTERS().
OK, we’ve expanded. Now on to the filters!
The first filter says, “hey, now that we’ve thrown out all time filters, let’s filter time back down to just be last year.”
FILTER(ALL(Periods),
Periods[Year]=MAX(Periods[Year])-1
)
Let’s talk about the FILTER() function itself for a moment.
How does FILTER() Work?
Honestly this function has deserved its own post for a long time. I’ll give a brief explanation here.
The syntax for the FILTER function is FILTER(TableToFilter, FilterExpression). Pretty simple. Here’s some more detail:
- FILTER() takes a TableToFilter and a FilterExpression, and returns all rows from that TableToFilter that match the FilterExpression.
- In the example above, TableToFilter is ALL(Periods)
- and FilterExpression is Periods[Year]=MAX(Periods[Year])-1
- FILTER() steps through the TableToFilter one row at a time.
- And for each row, it evaluates the FilterExpression. If the expression evaluates to true, the row is “kept.” If not, it is filtered out.
- Because FILTER() goes one row at a time, it can be quite slow if you use it against a large table. When I say “large” that is of course subjective. A few thousand rows is fine in my experience. A million is not. Do not use FILTER() against your fact table.
- The FilterExpression typically takes the form of Table[Column] = <expression>
- The comparison operator doesn’t have to be “=”. It can also be <, >, <=, >=, <>
- The expression on the right hand side of FilterExpression can be “rich.” This is VERY useful. In a simple CALCULATE, the right side of each filter expression has to be simple, like a literal number (9) or a string (“Standard”). The fact that FILTER() allows for rich expressions here is one of the most common reasons I use FILTER().
- The Table[Column] in the filter expression is a column in the TableToFilter. If you are filtering the Periods table, it makes sense that you are testing some property of each row in Periods. I can’t think of a sensible reason to use a column here that is NOT from TableToFilter. (Insert “boot signal” here, maybe the Italians can address this).
- FILTER() ignores everything else going on in your formula and acts completely on its own.
- For example, our overall formula sets ALL(Periods) as the first argument to CALCULATE.
- The FILTER()’s that come after that do NOT pay any attention to other arguments however, including that ALL(Periods).
- In other words, the FILTER() functions are still operating against the original filter context from the pivot! If the pivot is sliced to Year=2009, then the FILTER() function starts with the Periods table already pre-filtered to just 2009.
- This is why each of my FILTER()’s uses ALL(Periods) for TableToFilter. I have to repeat the “expand” step so that my FILTER() is also working from a clean slate.
- Even though each FILTER() operates on its own, their results then “stack up” in the overall formula.
- Even though FILTER() RETURNS a set of rows that matched the FilterExpression, it actually REMOVES rows from the overall filter context.
- This sounds tricky but really it isn’t.
- Let’s say our TableToFilter contains 6 rows: A, B, C, D, E, and F.
- And our overall formula contains two FILTER() clauses that both operate on the same TableToFilter, just like our overall formula near the beginning of this post.
- Let’s also say that the first FILTER() returns rows A, B, C, and D.
- And the second FILTER() returns rows C, D, E, and F.
- The net result is that only rows C and D are left “alive” in the overall filter context of the formula.
- So one way to think of this is that FILTER()s “stack up” on top of each other.
- Another way to think of it is that even though the first filter RETURNED rows A, B, C, and D, its real effect was to REMOVE all other rows (E and F) from consideration.
OK, back to that first filter!
Here it is again:
FILTER(ALL(Periods),
Periods[Year]=MAX(Periods[Year])-1
)
Let’s revisit points 1-5 above for this FILTER expression to see how it all works. And let’s examine just a single cell of the pivot to see how this FILTER operates for that one cell:
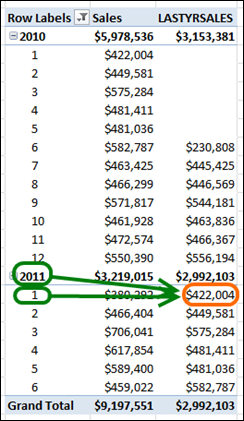
Focusing on The Orange-Circled LASTYRSALES Cell As An Example
With Its Period Filter Context Highlighted in Green
In that picture above, the orange cell we are looking at has a filter context “coming in” from the pivot. It has Period[Year] set to 2011 and Period[MerchPeriod] set to 1, as highlighted in green.
Given the detailed description of FILTER() from points 1-5 above, we can see that:
- We set ALL(Periods) as our TableToFilter so that we are starting from a clean slate with respect to time. So our Periods table now has “all rows alive.”
- Then our FilterExpression tests against the Periods[Year] column.
- MAX(Periods[Year]) – 1 still operates independently!, so it still picks up Periods[Year]=2011 from the pivot. Therefore it returns 2011 – 1 = 2010!
- Since we started with ALL(Periods) as the TableToFilter, and the FilterExpression only “keeps” rows where Year=2010, we are left with all 2010 rows “alive” after evaluating this FILTER().
- If we didn’t do ALL(Periods) for TableToFilter, and instead just used Periods without the ALL(), our FILTER would start out with only rows from 2011 (since that is what the pivot is telling us).
- And then in the next step when we go back a year to 2010, FILTER() would find no rows. There are no rows that match Periods[Year] = 2010 and Periods[Year]=2011.
- So our FILTER would return no rows, which means it would have the effect of REMOVING all rows from Periods in the overall formula, and our measure would return blank for all cells in the pivot.
That’s a lot of explanation, I know. Walk through it a few times. It’s actually pretty intuitive once you’ve done it a few times. The tricky part, for me, was discovering all of these details for myself. And since I’ve done all of that, you don’t have to.
That’s enough for this time. I think you can probably figure out how the second FILTER() evaluates based on the above, but I will step through it next time.
I will also explain why we use that last VALUES() in the formula, and probably also share some of the answers I got from the Italians, and from David Churchward, in response to my question “did I need to add that calc column in the Periods table?”